今日は、棚板の耐荷重について考えてみます。
筆者は建築士ではありますし、設計事務所ではあるのですが、意匠系の設計がメインになるため、構造的なお話は正直なところ専門外です。 😣
建築歴自体は長めですので、いつも経験値だけで何となく分かってしまうため、特に安全性に大きな影響のない部分の造作については、その100%の主観だけで決めてしまうのですが、実際のところはどうなんだろう・・・ということで、力学的な根拠を整理してみようと思い立った次第です。😅
今回は、可動棚に設置する棚板の耐荷重の考え方について、実際の耐荷重計算の計算例を4パターンほどご紹介しつつ、整理していきます。👌
例によって、長めの投稿になりますので、必要に応じて、以下の目次より該当箇所にジャンプして頂けると幸いです。😊
前置き
1年半ほど前に、可動棚の作り方を解説する投稿を書いたのですが、その投稿の中でご紹介した可動棚に使用した部材寸法(棚板の厚みや巾)を元に進めさせて頂きます。
元の投稿[DIYで可動棚を作りません?1]
また、しつこいようですが、構造は基本的に専門外ですので、30年ほど前の記憶と文献を掘り起こしながらの調査や検証を行い、何となく思い出してきたところではあるのですが、構造専門の方から見ると甘い部分があるかもしれません。
この点については予めご了解いただくと共に、何か根本的な不備などありましたら、コメントなどにてご指導いただけると有難く思います。😌
棚板の耐荷重について
棚板の耐荷重については、バキッと折れてしまう破壊強度ではなく、「たわみ」に着目します。
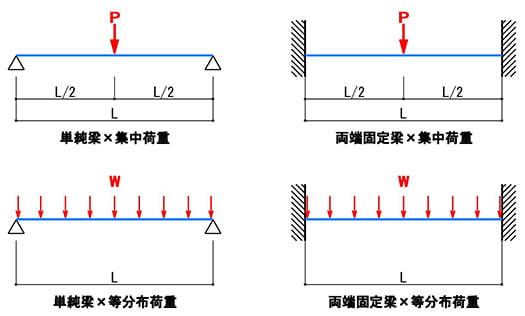
この「たわみ」を検討するに当たって、棚板を「梁」と呼ばれる部材に見立てるわけなのですが、基本的な支持形式として、「単純梁/両端固定梁」という二通りの考え方が存在します。
また、この「梁」に掛かる荷重の形式(種類?)として、「集中荷重/等分布荷重」という二通りがあります。
棚板の耐荷重には、もちろん棚板の厚みも関係はするのですが、ただ厚みを厚くすればいい!っていう訳ではありませんからね!😅
詳しくは後述していきます。👍
ちなみに、棚板の厚みは「断面二次モーメント:I」の項で、この耐荷重の計算にじみぃ~に(地味に)絡んできます。
片持ちや何やら・・・細かく分けるともっと沢山あるのですが、書き出すとキリがありませんし、そもそも専門外ですので、細かい話はご専門の方に譲ることにして、棚板の耐荷重という観点での基本的な内容までのご説明とさせていただきます。
その他、ご説明すべき用語については、後半で「その他の必要な用語」ということでまとめさせて頂くことにして、まずは、梁と荷重の形式辺りのご説明から入ろうと思います。
計算のやり方だけが知りたいんだ!😲という方は、大変お手数なのですが、右下のボタンから直接ジャンプして頂ければと思います。
梁の形式(単純/両端固定)
では、棚板と見立てる梁の形式のお話です。
前掲の図で言いますと、左👈の列が単純梁、右👉の列が両端固定梁になるのですが、左👈の単純梁からご説明していきます。
※「P」が荷重を示していまして、これは後述する「集中荷重」になります。

両端が支点ということになり、青の横線が「梁」となるのですが、△で表記されているものは「ピン」と呼んでたと思いますが、固定されていない(載っているだけの)支点を示しています。
今回は可動棚のお話がメインですが、両端が固定されておらず棚受け金物に載っているだけという意味では、固定されていない支点ということになりますので、この単純梁のモデルが、まさに可動棚の棚板の状態に近いモデルということになると思います。
この場合の「たわみ」を求める公式は、「たわみ」を「δ」としますと以下のようになります。
1)δ=P×L^3/48×E×I
「E」と「I」については、それぞれ後述する「ヤング係数」と「断面二次モーメント」ですので、その数値が入ります。
次に、以下の絵は、三角ではなく両側が壁的な形状になっていまして、この場合は固定された支点を示していることになりますので、こちらが「両端固定梁」のモデルです。
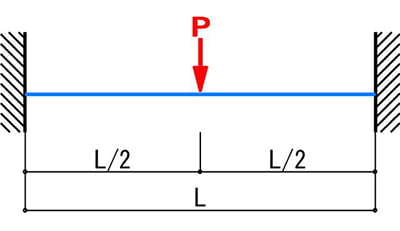
既述の単純梁の場合と同様、「たわみ」を「δ」としますと、公式は次のようになります。
2)δ=P×L^3/192×E×I
この両端固定梁のモデルは、棚で言いますと、可動ではない棚と言いましょうか・・・
例えば、小学校の下駄箱や銭湯のロッカーのように、棚板が側板に固定されてしまって動かせないような、両サイドが固定された棚の場合は、このモデルに近い状態ということになります。
公式の方に着目して頂いて、前者の単純梁の公式と見比べてみていただくと、分かりやすいのですが、分子は同じ数値で、分母については単純梁の方が小さくなりますので、たわみ量としては、単純梁の方が大きく、両端固定梁の方が小さくなることがご認識いただけるかな、と思います。🤔
荷重の形式(集中/等分布)
前項で絵を出してしまいましたが、梁の長さ(支点間距離=スパン)「L」に対して、その中央のみに全荷重が掛かると仮定したモデルが、前図👆にて赤で示した「P」の集中荷重です。
これに対し、この梁の長さ「L」に一つの荷重が全体的に分散されて掛かると仮定したモデルが、以下👇の図の赤で示した「W」の等分布荷重ということになります。
※前項の前者に当たる単純梁に掛かる等分布荷重。

この単純梁に掛かる等分布荷重による「たわみ」を求める公式は以下👇の通りです。
3)δ=5×W×L^4/384×E×I
前項でご紹介した集中荷重の場合の公式と比べますと、大きく違うのが、分母が三乗ではなく四乗になっている点です。☝
両端固定の場合の図も忘れないうちに、貼っておきますが、この等分布荷重が両端固定梁に掛かる場合は、以下👇のようなモデルになります。
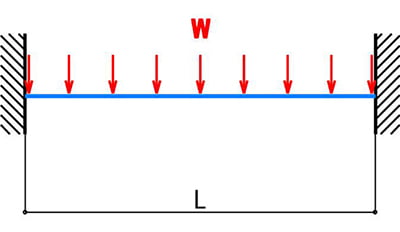
この場合の「たわみ」の公式としましては、次のようになります。
4)δ=W×L^4/384×E×I
両者の等分布荷重の公式を見ますと、今回は分母は同じで、分子の方が両端固定の場合の数字の5倍が、単純梁の分子になっていますので、この場合もやはり単純梁のモデルの方がたわみ量は大きくなるということが分かります。😉
近いモデルとしましては、以上の4パターンになるわけですが、今回のテーマは、棚板の耐荷重を考える・・・ということになっていますので、具体的にどのモデルをどんなパターンに当てはめて考えるべきなのか?ということで、今一度、棚板の話に戻します。

実際に、棚板中央1点に荷重が掛かると考える集中荷重が適切なのか、もしくは分散された一つの荷重が全体的に掛かると考える等分布荷重の方が適切なのか・・・
という観点では、棚板に載せるものによっても違ってくるとは思うのですが、真ん中だけに10kgの一つのモノを載せるケースよりは、例えば、500gの本×20冊を全体的に載せるケースの方が、圧倒的に現実的だと思われますので、モデルとしては、おそらく後者の等分布荷重が適切ですよね?🤔
でも「耐荷重」の検討という観点ではどうでしょうかね?👀
荷重モデルとしては等分布の方が適切な気はするものの、既述の通り、たわみ量の数字としては有利側の数字が出てくることになりますよね・・・
どこまで耐えうるのか?という意味での「耐荷重」の検討ですので、個人的には、モデル化の健全性よりも、まずは安全側の数字で当たってみる方が妥当な気がします。😑
あんまりひどい数値が出たら、もちろん等分布に逃げるかもしれないですけど・・・ 😅
その他の必要な用語
支点や荷重モデルの考え方と「たわみ」の公式について、ザッとお伝えしてきたところですが、実際にこの公式を使って棚の耐荷重計算(たわみ量の計算)を行おうとした場合、知っておかなければならない各記号や、単位の換算について、もう少し説明します。
ヤング係数(弾性率):E
これは聞かれたことがあるのではないかと思うのですが、「弾性率」とも呼ばれている、いわゆる「ヤング係数」です。
平たく言うと、材料の固さを示す係数になります。☝
建築の構造体に使われるような樹種であれば、ある程度決まった数字が見つかるのですが、元投稿で使用した材料は通称「シナランバー合板」というもので、
構造体に使用されるような代物(しろもの)ではなく、JAS規格でも「造作用LVL」という範疇に入る材料ですので、一般的に出回っている数値などは存在しないようで、生産している工場などでの試験結果による数値を見てみるしかないようです。
JAS規格の方も調べてはみたのですが、この「造作用LVL」については、強度に関する規格は定められていないようでした。😓
また、色々と嗅ぎまわった結果、強度的な試験をしていない工場も多々あるようですので、容易に入手できる数値ではないみたいですね・・・。
また、JAS規格上「普通合板」に該当するという見解もあったのですが、日本合板工業組合連合会さんというサイトに問合せを入れてみた結果、最終的にシナランバー合板は「造作用LVL」に該当するという回答でしたので、補足しておきます。🙏
今回は元投稿の方でもご紹介している、筆者が棚板関係をいつも注文している「木材 DIY 北零WOOD」さんでは、「参考値」として試験結果をお出しいただけましたので、この数値を元に計算することができました。
※筋違いなお願い以外は大抵クリアしてくれますので、非常に頼もしいショップさんです。

具体的な試験結果「曲げヤング係数」の数値としましては、平均値4000~5200Mpaとのことのことでしたので、不利側にみて、ヤング係数:E=4000Mpaと考え、実用上、製品性能のバラツキ等も考慮しまして、安全率を0.8としますと・・・
4000×0.8=3200Mpaになりますので、この実用上のヤング係数としてE=3200Mpaを採用することにします。
ヤング係数は、筆者の勉強不足だとは思うのですが、WEBで当たってみる限り、色んな数値が出回っているように感じました。
試験方法などによる違いとか、基準を定めている機関の違いとかなのでしょうかね・・・
木材は繊維方向がありますので、そういう違いもあるのかもしれません。
掲載されている樹種が最も多く、筆者的に認識しやすかった資料の数値からご紹介させて頂くことにしますが、木材関連のヤング係数については、置賜木さんサイトのこちらのPDFが分かりやすかったです。👍
単位については、「Gpa」表記になっていますので、先の「Mpa」と比較しようとすると、換算が必要なのですが、平たく言えば、例えば先ほどの「4000Mpa」から、ゼロを3つなくした「4」がGpa表記の数値になりますので、「4000Mpa=4Gpa」という換算になります。
※要するにMpa表記の数字を1000で割ればGpa表記になります。
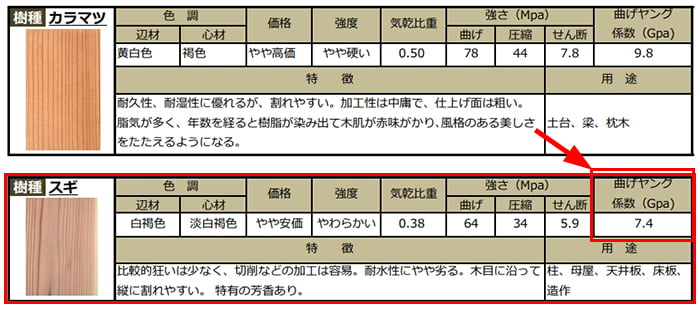
一般的な建築で使われる樹種があんまり見当たらないのですが、例えば杉は7.4Gpaとの記載。
桧(ヒノキ)は掲載がなかったのですが、手元の資料によると1000kg/mm^2ですので、9806.65N/mm^2(=Mpa)・・・、つまりMpa→9.80Gpaです。
その他、栂(ツガ)やSPFの数値もご紹介したかったのですが、明確な資料が見つかりませんでしたので、断念してしまいました。😅
※でも、たぶんSPFは杉と同じくらいだとは思います。
話のニュアンスはやや逸れるのですが、木材以外の数値も何点かご紹介しておきます。
プラスチック系の素材のヤング係数については、華陽物産さんサイトのこちらのPDFが何かと役に立ちそうです。 👍
ただ、建築しか知らない筆者にとっては数が多すぎて、知らない素材が多くて、棚板なんかに使われることのある「アクリル」や「ポリカ」を見つけ出すのに、ちょっと大変でした。😓
二枚目の1、2列目がアクリルで、4列目がポリカ。
ヤング係数については、上から12行目の「弾性率」欄に表記されている数値になるようです。
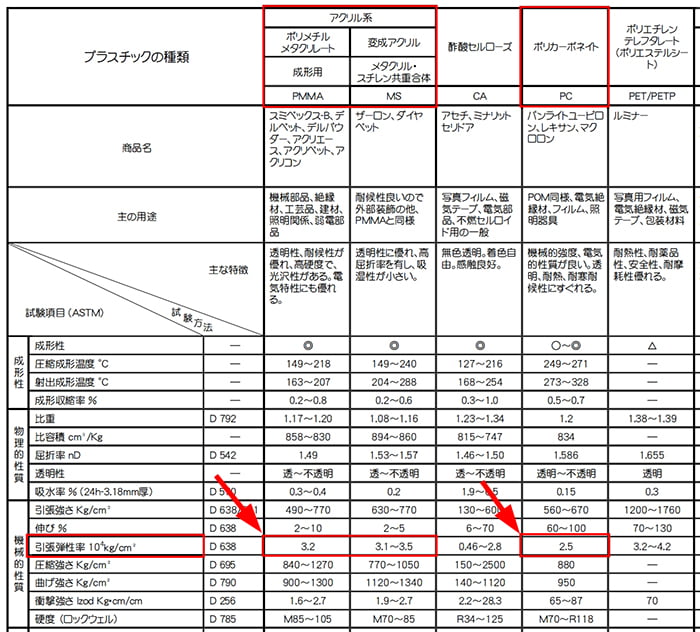
具体的な数字としては、アクリルが「3.1~3.5」、ポリカが「2.5」。
また、単位は「10^4kg/cm2」とのことですので、上述の数値に合わせるため、Gpa表記に直しますと、それぞれ約3.0~3.4Gpa、約2.4Gpaとなります。
その他、アルミやガラスは約72Gpa、ステンや鋼材は約205Gpa。
コンクリートは・・・
と、さらっと書きたい所だったのですが、設計基準強度により数値の増減があるため、またちょと分かりにくくなってしまいます。😣
結論を言うと、以下の式で求められるようです。
Ec=3.35×104×(y/24)^2×(Fc/60)^(1/3)
Ec:圧縮ヤング係数、y:気乾単位重量、Fc:設計基準強度
※普通コンクリートの場合:18≦Fc≦60がこの公式になるそうです☝
1/3乗の計算の仕方が分かりませんが、設計基準強度Fc21で考えた場合、こちらのサイトさんの計算では約21700N/mm2になるようですので、またGpa換算すると約21.7Gpaですよね。😉
よくは分らないのですが、概ね呼称の数字になるようですので、建築で使われるFcで考えますと、Fc21~Fc30くらいが相場と考えますと、約20~30Gpaほどということで良さそうです。
以上をザッとですが、参考までのヤング係数の値としてまとめますと、以下のような感じになります。
| 材料 | ヤング係数(Gpa) ※およその数値 |
| シナランバー合板(参考) | 4.0~5.0 |
| 木材:杉(スギ) | 7.4 |
| 桧(ヒノキ) | 9.8 |
| アクリル | 3.0~3.4 |
| ポリカーボネート | 2.4 |
| アルミ、ガラス | 72 |
| ステンレス、鋼材 | 205 |
| コンクリート(Fc21~30) | 20~30 |
断面二次モーメント:I
学生時代も建築士の試験勉強の時でも、大っ嫌いだった概念なのですが、「断面二次モーメント」という概念があります。😑
苦手な話ですので、ザッとにさせていただきますが、曲げようとする力が掛かった際の材料の曲がりにくさ、と言いますか、その力に対する抵抗性という感じの概念です。
この「たわみ」計算上では、断面二次モーメント:I=bh^3/12でいいようですので、ちょっと感じの悪い🤨印象ですが、以上とさせて頂きます。😑
「b」が奥行ですので、要するに棚板の奥行の数値で、「h」が厚みになりますので、棚板の厚みの数値が入ります。
・・・ですので、ここで「棚板の厚み」が地味に、棚板の耐荷重計算に影響することがお分かりになられると思います。😅
詳細については、建築学生が学ぶ構造力学さんサイトのこの辺りが分かりやすいかと思います。👌😊
単位の換算について
構造系の計算をする際に気をつけなければならないのは、単位の換算です。
これを間違えると、トンチンカンな数字が導き出されてしまいますので、主要なものだけ以下に整理しておきます。
- キログラム → ニュートン換算
1kg → 9.80665N - ヤング係数の単位換算
1)N/mm^2 = Mpa
2)1kgf/mm^2 = 9.80N/mm^2
3)1N/mm^2(Mpa) = 10.197kgf/cm^2
4)1N/mm^2 = 100N/cm^2
5)1000Mpa(=N/mm^2) = 1Gpa
※すごく紛らわしいですよね。統一してほしいものです。😒
棚板の耐荷重計算のやり方と計算例
さて・・・
相変わらず前置きが長くなってしまいましたが、基本事項は概ねお伝えできた気がしますので、実際の棚板の耐荷重計算、つまりたわみ量の計算に移っていこうと思います。
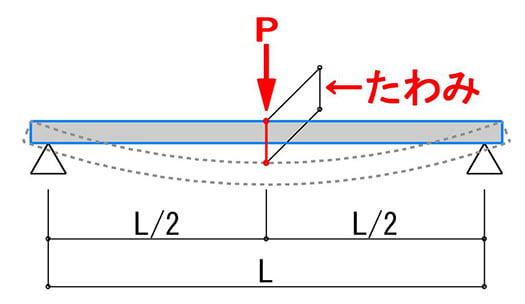
(耐荷重検討の計算イメージ)
既述の通り、モデル化の健全性というよりは、安全性の観点より、(できれば)不利側の数値を採用したいことから、モデルとしては既述の「1)」単純梁の中央のみに集中荷重が掛かるとした場合の公式を用いて、たわみ量をチェックしてみることにします。
1)δ=P×L^3/48×E×I
ちなみに、建築基準法関連の基準では、たわみ量:δ=L/250(L/300)以下となってはいますが、今回の棚板は建築の一部ではあるものの、大きく安全性に影響のある部分ではありませんので、あくまでも目安程度と考えることにします。
耐荷重計算に使用する数値の確認
まずは数値の確認、単位の確認、及び準備計算です。
[棚板の寸法]
具体的な部材は既述の通り、元投稿[DIYで可動棚を作りません?1]で採用したものを使いますので、この辺りより、棚板自体の寸法は巾735mm×奥行450mm、厚みは18mmになるわけですが、具体的に、これらの数字がどこに当てはまるかと言いますと・・・
以下👇の「梁」の断面スケッチを、まずご覧ください。🧐
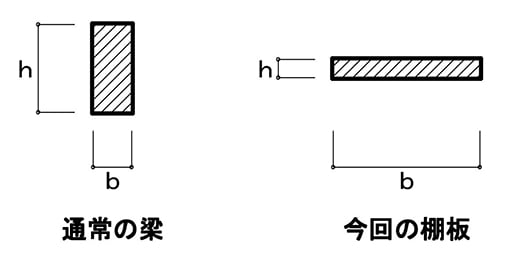
棚板を梁に見立て、梁のたわみ量から想定する訳ですので、通常は左側の断面より、縦長のbh寸法を使うことになるのですが、今回は棚板ですので、縦長でなく右側👉の横長のbh寸法を使用することになります。
つまり、支点間距離「L」については「巾735mm」、梁の奥行に当たる「b」については「奥行450mm」、梁の背に当たる「h」については「厚18mm」が当てはまります。
[Check]☝
mm単位ですと、数値が大きくなりすぎて計算がやりづらくなるため、ここでcm単位に変換してしまいましょう。
つまり、L=73.5cm、b=45cm、h=1.8cmを実際には採用します。
断面二次モーメントは前掲の通り、I=bh^3/12ですので、ここにbhの数値のみを当てはめて求めることになります。
cm換算してから、実際に当てはめてみますと、結果、I=450×18^3/12=21.87cm^4ですので、この数値を、後ほど1)の公式に入れ込む数値とします。
[ヤング係数]
前半で宣言しました通り、ヤング係数については「木材 DIY 北零WOOD」さんより、「参考値」としてご提供いただいた試験結果を採用することにするのですが、既述の通り、実用上の安全率を考慮した値、E=3200Mpaを採用します。
※あくまでも参考値になりますので、絶対的な数字ではありません。
ただ、前項でcm単位に変換してしまいましたので、メンドくさくてイヤになるのですが、これを「kgf/cm^2単位」に変換せねばなりませんよね。😴💦
前々項辺りの「単位の変換」、3)1N/mm^2(Mpa)=10.197kgf/cm^2より変換しますと、実際に入れ込む数値は・・・、
3200×10.197=32630.4ですが、少し丸めさせて頂き、E≒32500kgf/cm^2とします。
[想定荷重]
荷重については、元投稿[DIYで可動棚を作りません?1]の中で、この項の後半より、 「15kg×6枚なら・・・」と100%の直感だけで書いていますが、この筆者の直感と力学的な数値の食違いも知りたいところではありますので、とりあえずは、この「15kg」を採用してみることにさせてください。🙏
前項にて、採用するヤング率の単位は「kgf/cm^2」に変換したところですので、ここでは、そのままの数値P=15kgf/cm^2を採用することになります。
さあ!ようやく主要な数字が出そろって参りました🤣ので、いよいよ!実際の計算に入っていきます。👊
実際の耐荷重計算(単純梁×集中荷重)
まず、単純梁×集中荷重のモデルと、公式、1)を確認しておきましょう!
既述の通り・・・、
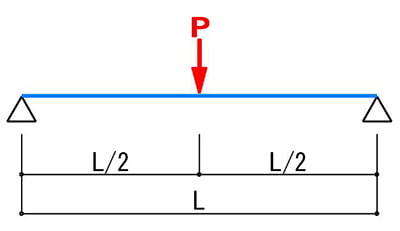
(たわみ量によるモデル1)
1)δ=P×L^3/48×E×I
ですので、この公式に対して、前項で準備しておいた数字を入れ込んでいきます。😉
δ=15×73.5^3/48×32500×21.87
ですので、これを電卓で計算しますと、=0.174574になりますよね?🤔
単位はcm単位にしてありましたので、要するに「約0.174cm」・・・、つまり「約1.74mm」のたわみが生じる!という結果になりました。🤗
途中で「あまり気にしないことにする」と宣言した、建築のたわみ量の基準を念のため確認しておきますと、「たわみ量:δ=L/250(L/300)以下」でしたので、L=735mmとしますと、δ≦2.94mm(2.45mm)になり・・・、
結果、今回のたわみ量:1.7mm ≦ 基準たわみ量:2.45mmですので、建築的にもまだ余裕がある、ということになります。👍
モデル化した単純梁×集中荷重での結果ですので、実際のたわみ量との差は当たり前に出てしまうのですが、一つの目安にはなりますので、換算がややメンドくさいのですが、参考にして頂ければと思います。😌
なお、個人的にもちょっと興味がありましたので、その他のモデルでの計算も、次項以下にて、参考までにご紹介しておきます。
追加1(両端固定×集中荷重)
両端固定梁に集中荷重が掛かると仮定した場合の計算例です。(モデル2)

(たわみ量によるモデル2)
公式は・・・
2)δ=P×L^3/192×E×I
でしたので、前項までに仮定した具体的な数値を当てはめますと、以下のようになります。
δ=15×73.5^3/192×32500×21.87
これを計算しますと、=0.043643。
単位はcmですので、同様にmm単位にしますと、「約0.43mm」のたわみが生じるという結果になるということですね。
単純梁に比べますと、だいぶ数値が小さくなりますので、棚板として見た場合、両端を固定した方が耐荷重がぜんぜん上がる・・・ということがお分かりになられると思います。🤔
追加2(単純梁×等分布荷重)
次に単純梁に全体的な等分布荷重が掛かる場合の計算例です。(モデル3)

(たわみ量によるモデル3)
等分布荷重の場合、荷重は「P」ではなく、「W」になりますので、ちょっとだけニュアンスが変わりまして、準備計算としては、73.5cmの梁の1cm当りに掛かる数値を算出する必要があります。
ですので、集中荷重で使った「15kg」を「L」の長さ73.5cmで割ることになり、15÷73.5ですので、等分布荷重「W」としては0.204kgf/cm^2が導き出され、これを入れ込むことになる訳です。😉
公式については、既述の通りですが・・・
3)δ=5×W×L^4/384×E×I
でしたので、同様に具体的な数字を当てはめてみますと、以下のような計算をすることになります。
δ=5×0.204×73.5^4/384×32500×21.87
電卓でこれを計算しますと、=0.109065cm。
つまり、モデル3の単純梁×等分布荷重で考えた場合に想定されるたわみ量は「約1.09mm」ということです。
集中荷重の場合は1)で「1.74mm」でしたので、これよりはたわみは小さいということですので、実際にはケースバイケースにはなるとしても、棚板の耐荷重としては1.6倍弱くらいには上がると考えて良さそうです。
追加3(両端固定×等分布荷重)
最後に、両端固定梁に全体的な等分布荷重が掛かる場合の計算例です。(モデル3)
今回ご紹介している、四つのモデルの中ではたわみ量が最も小さくなるモデルですので、有利側のケースということになります。

(たわみ量によるモデル4)
これも既述の通りですが、公式は以下になります。
4)δ=W×L^4/384×E×I
これに同じように、仮定した数字を入れ込む訳ですが、等分布荷重ですので、前項と同様に「W」には「0.204」を当てます。
δ=0.204×73.5^4/384×32500×21.87
前半で公式の違いを見ましたが、前項のモデル3の公式の分子が1/5になるだけですので、電卓計算はちょっと端折りまして、単純に前項の0.109065を5で割った数字がたわみ量と考えます。
※ちょっとメンドくさくなってきてしまいましたので。😅
つまり、0.109065÷5=0.021813。
cmをmmに換算して、たわみ量としては「約0.22mm」ほど、という結果になりますので、両端固定梁×等分布荷重のモデルでは、実際のたわみ量は別として、計算上はほとんどたわまない、という結果になるということです。🤗
※あくまでも計算上の話です。☝
モデル2~4でご紹介した形の想定ですと、計算上のたわみ量としましては、モデル1:単純梁×集中荷重の場合に比べて、だいぶ低く出てはくるのですが、実際の棚板として考えますと、現実的にはたわみます。
・・・というか、いずれは、計算上の数値を超えて撓んでくる(たわんでくる)ものとお考えください。
ですので、棚板の耐荷重を考えるという意図で、このたわみ量の計算をされる場合は、途中でも何回か書いてきましたが、単純梁×集中荷重のモデル1の形で不利側に見ておくようにしていただいた方が、間違いありません。👍😉
今日のまとめ
本日は、棚板の耐荷重について考える・・・ということで、棚板を梁に見立てて行う、たわみ量の計算をご紹介して参りました。
可動棚のような、両端が固定されていない棚板と比べると、両端が固定された棚板の方がたわみ量が少なく、(あくまでも計算上は)耐荷重的にも大きくなりそうであることがお伝えできたかな・・・とは思うのですが、いずれにしても、ここで考えた棚板の耐荷重の検討だけで、棚全体の耐荷重が決まる訳ではありません。

可動棚であれば、棚柱の耐荷重やそれを固定するビスやボードピンの強度、それらを打ち込む下地材や面材の強度、棚ダボの耐荷重なども絡んできますし、固定棚の場合であっても、その棚板を固定する金物や固定の仕方、側板の強度などが色々と絡んでくるものですので、一概には「これで大丈夫!」とは言い切れないものと、筆者は考えています。
最後にちょっと否定的なお話になってしまいましたが・・・ 😓
今回ご紹介した、たわみ量の計算は、棚板の耐荷重をイメージする上で、少なくともひとつの目安にはなることは間違いありませんので、部材選定の際に、何かしらの参考になれば幸いです。😏
長くなりましたが、本日も最後までお読みいただき、どうも有難うございました。🙌



コメント
詳しい記事で大変参考になりました。
計算式をエクセルに起こして、必要事項を記入すればたわみ値が出るようにしました。
テーブルや踏み台、棚などあらゆる場面で役に立ちそうですので目安として使用させて頂きます。
コメント有難うございます。
そうですよね!
エクセルにして配布するか?サイト上で計算できるようにすると便利だろうと思って、こちらでも一度は試みたのですが、やり方が分からず・・・
断念してしまいました(苦笑)
ちょっと不親切な記事のままになってしまっていて、大変恐縮なのですが、お役に立てそうならよかったです。